Optimal cutting of materials

One of the important factors in improving industrial production efficiency is the conservation of material resources. Conserving materials is a rather complex task, requiring consideration of design, technological, and organizational factors. Careful analysis of each of these factors allows for the development of various methods and tools that facilitate resource savings. One of the effective means providing significant (up to 20%) material resource savings is their optimal or rational cutting. In practice, material resources are most often presented in the form of rolls (Fig. 1), strips, rectangular sheets, rods, etc.

Generally, cutting, for example, sheet and long products includes choosing economically feasible options for placing blanks on the material or strips on sheets according to the selected order form, taking available equipment into account. An example of industrial equipment for cutting rolls is presented in Fig. 2.  

  

By optimal cutting, we mean cutting that, with this type of production, allows for the output of the final product with minimal labor, time, and material usage while using existing equipment. Consequently, the definition of optimal cutting is a complex multifactorial task. Even if we reduce the solution of this problem to the level of two-dimensional (2D) rectangular cutting, this task also falls into the class of NP-hard combinatorial optimization problems, meaning there is no polynomial complexity algorithm for its exact solution. Additionally, such a problem contains an NP-hard sub-problem. Therefore, when addressing this task, the use of exhaustive (exact) algorithms leads to a complete enumeration of all possible options, which often involves significant computer time costs, not always economically viable. Currently, there are cutting problem-solving methods based on various approaches that reduce the volume of calculations. In particular, great importance worldwide has always been given to the development and study of heuristic optimization methods, including so-called meta-heuristic methods, which are invariant relative to the type of problem.

However, considering the modern development of high-performance computing equipment (e.g., CUDA — Compute Unified Device Architecture), there are more opportunities for using exact algorithms, increasing accuracy in calculations. CUDA is a software and hardware architecture that significantly (by several orders of magnitude) boosts computer processing power by using graphics processors of the video module (graphics card). The graphics card architecture allows for data "parallelism" in processing. Furthermore, the exchange rate between memory and the video processor is much higher than in the classical scheme: RAM — cache — central processing unit. This is due to data parallelization — while one piece of data in the graphics card starts processing by one stream processor, other data is simultaneously loaded into another.

In the financial market, for example, companies Numerix and CompatibL, using CUDA in a software product designed to analyze counterparty risk, achieved an 18-fold speed increase. Numerix is utilized by nearly 400 financial institutions worldwide, including BNP Paribas in the banking sector.

NVIDIA's CUDA® is a parallel computing platform and programming model with a set of extensions for programming languages C and C++, which allows for the expression of data and task parallelism at the level of small and large structural units. This significantly simplifies the use of this technology for nesting and packing problems, enabling both exact and heuristic algorithms with significant (more than tenfold) reductions in computing time.

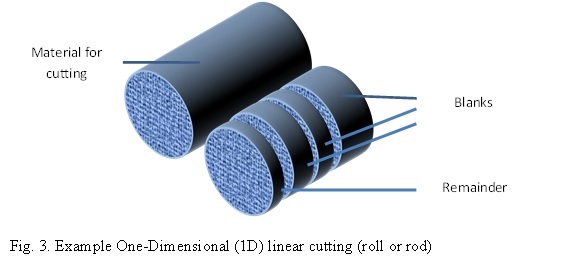
The simplest variant for determining optimal cutting is one-dimensional (1D) linear cutting (Fig. 3). Material for cutting into blanks of given sizes comes in identical rolls (rods, strips). In this case, a map of all possible cutting variants is created in one dimension (for instance, along the material's length or width), where the remainder in each variant is less than the length (or width) of the shortest (or narrowest) blank. When creating a cutting map, it is also necessary to account for such technological parameters of cutting equipment (stamping, etc.) as the thickness of the cut and the width of the side edges.

 

In this case, a standard-form mathematical model of the problem is usually compiled with a linear function (objective function) (1) reaching a minimum and a system of constraints (2), under conditions of non-negativity (3).

Then the system of linear algebraic equations is solved using the Jordan-Gauss method. A feasible solution where the objective function achieves a maximum (or minimum) will be the optimal solution. This algorithm is implemented in the software product "C-MES: Production Management" (hereafter C-MES). In C-MES, with 1D roll cutting, knife change optimization is also provided, i.e., further processing of the found solution is carried out to achieve the minimum number of knife changes.

The economic effect of using C-MES for linear cutting (rolls, rods, rails, etc.) includes:

• increase in the output of finished products (from 2% and above);
• reduction of equipment setup costs;
• reduction of production order fulfillment times (up to 10%);
• increase in planning speed.

Total savings, in this case, will be calculated by the formula:

S = SR + SW, 

where SR is the savings from reducing the material resource consumption rate, and SW is the savings on the wage costs of enterprise employees and the fees charged on their wages.

In the example of calculating the economic efficiency of the optimal cutting method for metalworking enterprises, it’s evident that as a result of applying the optimal material cutting method, the production cost is reduced by an average of 9.32%.

A significant interest presents the problem of two-dimensional (2D) rectangular nesting. This is due to the vast scope of practical application of these tasks, as well as the high complexity of the problem being solved. Due to the complexity of this task, heuristic decision algorithms are widely used in practice. The emergence and development of probabilistic local search methods for the optimum have led to the development of algorithms that serve as decoders in multipass algorithms.

Essentially, the placement of rectangles is reduced to their packing, where they do not intersect. Most exact methods for solving this problem involve searching the entire set of admissible solutions and finding the optimum among them. The search efficiency can be improved by applying various kinds of improvements. A large group of accelerated search methods is known as the "branch and bound method," which is a sort of complete enumeration. During calculations, sets (subsets) of admissible but non-optimal solutions are removed.

Depending on the current input data, one or another method of improving the search is selected, and preliminary preparation of the input data for the chosen sorting method is also carried out. These operations reduce computation time to an acceptable (economical) level. The conditions for placing the rectangles are described by a system of linear inequalities and the same number of integer variables. The resulting system of inequalities is solved using linear programming methods. In this case, the algorithm allows solving the problem of rectangular cutting accurately (or optimally). The result of this algorithm implemented in the software product "C-MES: Production Management" is presented in Fig. 4.

 

Additional optimization is also possible to increase the area of one of the remnants (fig. 5).

 

The economic effect of using C-MES for rectangular cutting is composed of the same components as for linear cutting. However, the increase in finished goods output can reach up to 10%, and the efficiency of plan creation can increase by 50%. This is explained by the fact that this type of cutting is a more labor-intensive operation, and in most cases, the result of planning such a task without using effective tools will not be optimal. Therefore, the economic effect of implementing C-MES for 2D nesting will be more significant with the optimal loading of equipment that allows for rectangular cutting (fig. 6).

 

When solving three-dimensional (3D) cutting (packaging) (3D) tasks, heuristic (approximate) algorithms are most often used. Any approximate solution assumes the existence of an algorithm that would allow exact determination of how to produce 3D cutting or place boxes in a container. They are basically built on decomposition—notation of these tasks into smaller tasks. Various variants of this procedure are applied—for example, splitting into layers and filling each layer according to an individual algorithm or "building walls." There are algorithms where after filling each layer or "building a wall" additional optimization is performed.

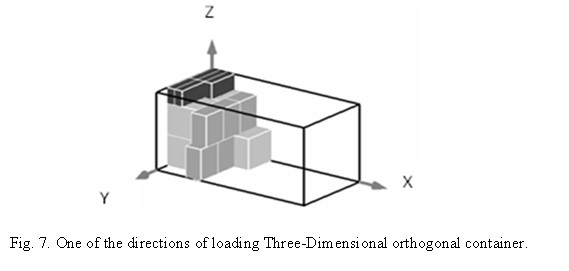
The number of precise algorithms for solving the three-dimensional nesting-packing problem is limited compared to the number of available heuristic optimization methods. One reason for this is the complexity of presenting possible packaging and imposing constraints on real problems. Nevertheless, various methods have been developed to solve this problem. For example, a model based on the Cartesian coordinate system provides vertical and horizontal stability and in most cases allows finding the optimal solution. The plane method for solving 3D cutting problems is theoretically justified. A version of the direction of loading a three-dimensional orthogonal container, using an example of implementing orthogonal packaging problem algorithms for objects, is shown in fig. 7.

In the C-MES concept, the definition of optimal 3D nesting is also used to solve the problem of cargo packing during transportation between production sites of the enterprise. 

 

Thus, the program (algorithm) of any (1D, 2D, 3D) cutting includes two basic steps: the stage of plotting the map of all possible nesting options and the step of calculating optimal nesting options.

Given the trend toward the widespread use of artificial neural networks (ANN) in recent years, it seems possible and even promising to use them for solving 3D cutting problems, despite the complexity and labor-intensiveness of training ANN.

It should be noted that in the world there are many software products for the formation of different types of nestings, but in general, they are supplied as separate solutions. C-MES is a comprehensive software product designed to perform the following functions:

• state control and resource allocation;
• production dispatching;
• data collection and storage;
• production personnel management;
• quality control;
• production process management;
• product tracking and genealogy;
• efficiency analysis.

The nesting function is integrated into C-MES and therefore allows calculating optimal cuts based on the current situation in a particular production based on real-time data, making it more economically efficient. These data are formed during monitoring and dispatching of the following production procedures (functions):

• management of needs and reproduction methods;
• calculation of packages for work centers with batch operation mode;
• formation of the production schedule, including consideration of supply chains;
• collection of execution facts;
• rescheduling taking into account deviations.

Considering the modularity of C-MES, the nesting module can be used both in conjunction with other modules and independently, providing flexibility in applying the nesting function in the current production environment. However, for effective interaction between production processes within the enterprise, it is more expedient to use nesting calculations in combination with the above functions.

C-MES is a complex business application designed to perform such large computational tasks as nesting tasks. Economically feasible time costs for solving 2D and 3D cuts can only be achieved using parallel computations implemented in several ways: either locally (for example, though not in all cases using CUDA technology) or using data centers (DC). C-MES can be supplied in both versions, while the second option (use of data centers in the SaaS model) for small and medium-sized enterprises is less expensive, allowing such companies to utilize large computing power, enabling all interested parties and departments to make effective decisions.